Обращение интервалов или волшебство на уроках сольфеджио

Обращение интервалов – это превращение одних интервала в другие путём перестановки верхнего и нижнего звука. Как известно, нижний звук интервала называется его основанием, а верхний – вершиной.

И, если, поменять местами вершину и основание, или, другими словами, попросту перевернуть интервал вверх тормашками, то в результате получится новый интервал, который и будет являться обращением первого, исходного музыкального интервала.

Как выполняются обращения интервалов?

Сначала разберём манипуляции только с простыми интервалами. Обращение выполняется путём переноса нижнего звука, то есть основания, на чистую октаву вверх, или перемещением нижнего звука интервала, то есть вершины, на октаву вниз. Результат получится один и тот же. Перемещается только один из звуков, второй звук остаётся на своём месте, его трогать не нужно.

Например, возьмём большую терцию «до-ми» и обратим её любым способом. Сначала, основание «до» перенесём на октаву вверх, у нас получится интервал «ми-до» — малая секста. Затем попробуем поступить наоборот и перенесём вниз на октаву верхний звук «ми», в результате также получаем малую сексту «ми-до». На картинке желтым цветом выделен звук, который остаётся на месте, а сиреневым – тот, который перемещается на октаву.

Ещё пример: дан интервал «ре-ля» (это чистая квинта, так как ступеней между звуками пять, а качественная величина – три с половиной тона). Попробуем сделать обращение этого интервала. Переносим «ре» выше – получаем «ля-ре»; или переносим «ля» ниже и тоже получаем «ля-ре». В обоих случаях чистая квинта обратилась в чистую кварту.

Кстати, путём обратных действий, можно вернуться к исходным интервалам. Так, сексту «ми-до» можно обратить в терцию «до-ми», от которой мы сначала отталкивались, ну а кварту «ля-ре» легко снова превратить в квинту «ре-ля».

О чём это говорит? Это говорит о том, что между разными интервалами есть какая-то связь, и о том, что существуют пары взаимно обращаемых интервалов. Эти интересные наблюдения легли в основу законов интервальных обращений.

Законы обращения интервалов

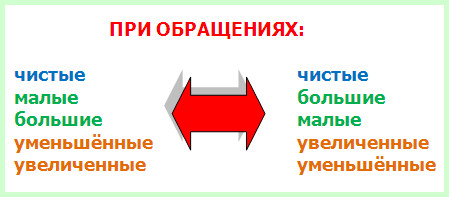
Мы знаем, что у любого интервала есть два измерения: количественная и качественная величина. Первая выражается в том, сколько ступеней охватывает тот или иной интервал, обозначается числом, и от неё зависит название интервала (прима, секунда, терция и другие). Вторая указывает на то, сколько в интервале тонов или полутонов. И, благодаря ей, у интервалов появляются дополнительные уточняющие названия из слов «чистый», «малый», «большой», «увеличенный» или «уменьшённый». Следует отметить, что оба параметра интервала меняются при обращении – и ступеневый показатель, и тоновый.

Законов-правил всего два.

Правило 1. Чистые интервалы при обращении остаются чистыми, малые превращаются в большие, а большие, наоборот, в малые, уменьшённые делаются увеличенными, ну а увеличенные интервалы, в свою очередь, уменьшёнными.

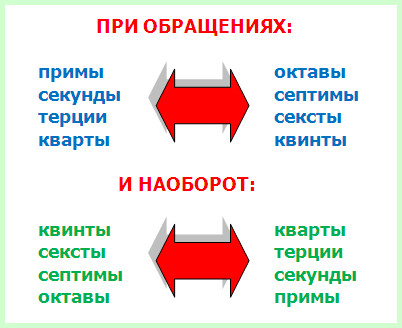
Правило 2. Примы обращаются в октавы, а октавы – в примы; секунды переходят в септимы, а септимы – в секунды; терции становятся секстами, а сексты – терциями, кварты перевоплощаются в квинты, а квинты, соответственно, в кварты.

Сумма обозначений взаимообращающихся простых интервалов равна девяти. Например, прима обозначается числом 1, октава – числом 8. 1+8=9. Секунда – 2, септима – 7, 2+7=9. Терции – 3, сексты – 6, 3+6=9. Кварты – 4, квинты – 5, вместе снова получается 9. И, если вдруг вы забыли, кто куда обращается, то просто из девятки вычитайте числовое обозначение данного вам интервала.

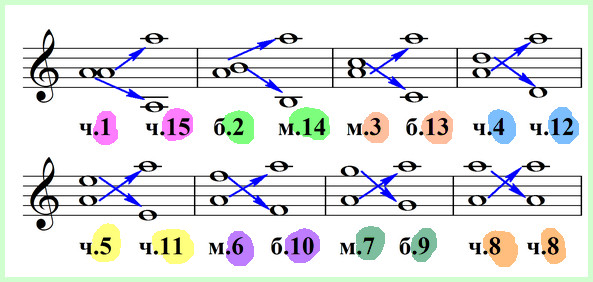
Давайте посмотрим действие этих законов на практике. Даны несколько интервалов: чистая прима от ре, малая терция от ми, большая секунда от до-диеза, уменьшённая септима от фа-диеза, увеличенная кварта от ре. Обратим их и выявим изменения.

Итак, после обращения чистая прима от ре превратилась в чистую октаву: тем самым находят подтверждения два момента: во-первых, чистые интервалы и после обращения остаются чистыми, а, во-вторых, прима стала октавой. Далее, малая терция «ми-соль» после обращения явилась как большая секста «соль-ми», что снова подтверждает уже сформулированные нами законы: малое выросло в большое, терция стала секстой. Следующий пример: большая секунда «до-диез и ре-диез» превратилась в малую септиму из тех же звуков (малое – в большое, секунда – в септиму). Аналогично и в других случаях: уменьшённое становится увеличенным и наоборот.

Проверь себя!

Предлагаем немного потренироваться для лучшего закрепления темы.

ЗАДАНИЕ: Дан ряд интервалов, нужно определить, что это за интервалы, затем мысленно (или письменно, если трудно так сразу) обратить их и сказать, во что они превратятся после обращения.

Фокусы с составными интервалами

Составные интервалы тоже могут участвовать в обращении. Напомним, что составными называются интервалы, которые шире октавы, то есть ноны, децимы, ундецимы и другие.

Чтобы получить при обращении из простого интервала составной, нужно переместить одновременно и вершину, и основание. Причём, основание – на октаву вверх, а вершину – на октаву вниз.

Например, возьмём большую терцию «до-ми», переместим основание «до» на октаву выше, а вершину «ми», соответственно, на октаву ниже. В результате такого двойного перемещения у нас получился широкий интервал «ми-до», секста через октаву, или, если быть точнее, малая терцдецима.

Подобным же образом, и другие простые интервалы можно превратить в составные и, наоборот, из составного интервала можно получить простой, если вершину его на октаву опустить, а основание поднять.

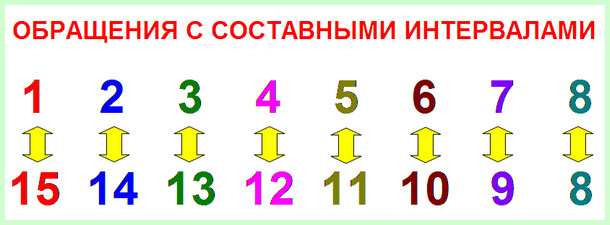
Какие будут соблюдаться закономерности? Сумма обозначений двух взаимообращаемых интервалов будет равна шестнадцати. Так:

• Прима обращается в квинтдециму (1+15=16);
• Секунда превращается в квартдециму (2+14=16);
• Терция переходит в терцдециму (3+13=16);
• Кварта становится дуодецимой (4+12=16);
• Квинта перевоплощается в ундециму (5+11=16);
• Секста оборачивается децимой (6+10=16);
• Септима предстаёт как нона (7+9=16);
• С октавой эти штуки не проходят, она обращается в саму себя и поэтому составные интервалы тут уже не причём, хотя красивые цифры есть и в этом случае (8+8=16).

Применение обращений интервалов

Не стоит думать, что обращения интервалов, так подробно изучаемые в курсе школьного сольфеджио, не имеют никакого практического применения. Напротив, это очень важная и нужная штука.

Практическая область применений обращений связана не только с пониманием того, как возникли некоторые интервалы (да-да, исторически некоторые интервалы были обнаружены путём обращения). Если брать теоретическую область, то обращения очень помогают, например, в запоминании тритонов или характерных интервалов, изучаемых в старших классах и в колледжах, в понимании устройства некоторых аккордов.

Если брать область творческую, то обращения широко применяются при сочинении музыки, причём иногда мы даже их не замечаем. Послушайте, например, кусочек красивой мелодии в романтическом духе, он весь построен на восходящих интонациях терций и секст.

Вы, кстати, тоже легко можете попробовать сочинить нечто подобное. Даже, если взять те же терции и сексты, только в нисходящей интонации:

---

P.S. Дорогие друзья! На этой ноте мы завершаем сегодняшний выпуск. Если у вас остались ещё вопросы об обращениях интервалов, то, пожалуйста, задайте их в комментариях к этой статье.

P.P.S. Для окончательного усвоения данной темы предлагаем вам посмотреть забавное видео от замечательного учителя сольфеджио наших дней Анны Наумовой.