В предыдущей заметке мы выяснили, как устроен звук. Повторим ещё раз эту формулу:
ЗВУК = ОСНОВНОЙ ТОН + ВСЕ КРАТНЫЕ ОБЕРТОНА
Кроме того, как японцы любуются на цветение сакуры, полюбуемся и мы на график АЧХ — амплитудно-частотной характеристики звука (рис. 1):
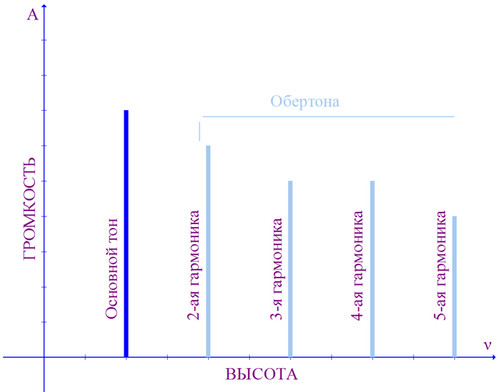
Напомним, что по горизонтальной оси отложена высота звука (частота колебаний), а по вертикальной – громкость (амплитуда).
Каждая вертикальная линия – это гармоника, первая гармоника обычно называется основным тоном. Гармоники устроены так: вторая гармоника в 2 раза выше основного тона, третья – в три, четвертая – в четыре и так далее.
Краткости ради вместо «частота n-ой гармоники» будем говорить просто «n-ая гармоника», а вместо «частота основного тона» — «частота звука».
Итак, глядя на АЧХ, нам не составит труда ответить на вопрос, что же такое консонанс.
Как досчитать до бесконечности?
Консонанс буквально означает «со-звучие», совместное звучание. Что же у двух различных звуков может звучать совместно?
Нарисуем их на одном графике друг под другом (рис. 2):

Вот и ответ: часть гармоник могут совпадать по частоте. Логично предположить, что чем больше совпадающих частот, тем больше у звуков «общего», а, следовательно, тем больше консонанса в звучании такого интервала. Если быть совсем точным, то важно не просто число совпадающих гармоник, а то, какая доля от всех звучащих гармоник совпадает, то есть отношение числа совпадающих к общему числу звучащих гармоник.
Получаем самую простую формулу для подсчета консонанса:
где Nсовп — число совпадающих гармоник, Nобщ — общее число звучащих гармоник (количество различных звучащих частот), а cons и есть наш искомый консонанс. Если быть математически корректным, то величину лучше называть мера частотного консонанса.
Что ж, дело за малым: нужно посчитать Nсовп и Nобщ, поделить одно на другое, и получим нужный результат.
Проблема заключается лишь в том, что и общее число гармоник и даже число совпадающих гармоник бесконечно.
Что же получится, если мы поделим бесконечность на бесконечность?
Поменяем масштаб предыдущего графика, «отдалимся» от него (рис. 3)
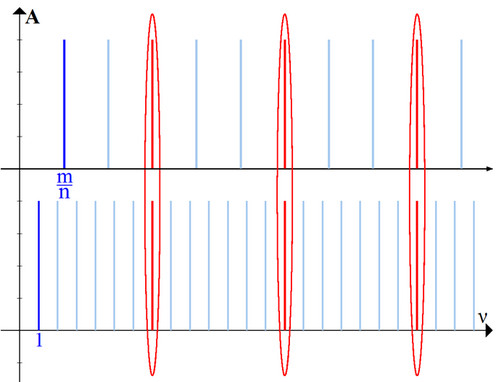
Мы видим, что совпадающие гармоники встречаются вновь и вновь. Картинка повторяется (рис. 4).
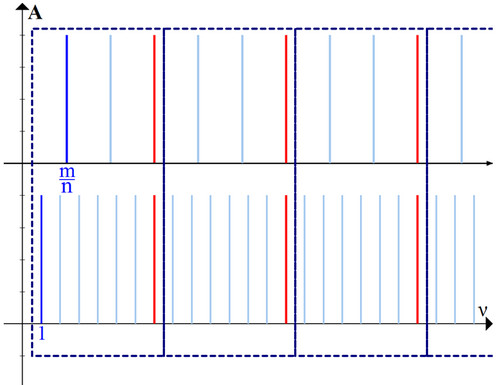
Это повторение нам и поможет.
Нам достаточно посчитать отношение (1) в одном из пунктирных прямоугольников (например, в первом), тогда из-за повторений и на всей прямой это соотношение останется таким же.
Для простоты частоту основного тона первого (нижнего) звука будем считать равной единице, а частоту основного тона второго звука запишем в виде несократимой дроби  .
.
Заметим в скобках, что в нотных системах, как правило, используются именно звуки, соотношение частот которых выражается какой-либо дробью  . К примеру, интервал квинты – это соотношение
. К примеру, интервал квинты – это соотношение  , кварты —
, кварты —  , тритона —
, тритона —  и т.д.
и т.д.
Посчитаем отношение (1) внутри первого прямоугольника (рис. 4).
Довольно легко посчитать число совпадающих гармоник . Формально их две, одна принадлежит нижнему звуку, вторая – верхнему, на рис.4 они обозначены красным. Но обе эти гармоники звучат на одной и той же частоте, соответственно, если мы считаем число совпадающих частот, то такая частота будет всего одна.
Чему же равно общее число звучащих частот?
Будем рассуждать так.
Все гармоники нижнего звука располагаются в целых числах (1, 2, 3 и т.д.). Как только какая-либо гармоника верхнего звука будет целым числом, она совпадет с одной из гармоник нижнего. Все гармоники верхнего звука кратны основному тону  , поэтому частота n-ной гармоники будет равна:
, поэтому частота n-ной гармоники будет равна:
то есть она будет целым числом (так как m – целое число). Значит, у верхнего звука в прямоугольнике находятся гармоники от первой (основного тона) до n-ой, следовательно, звучат n частот.
Поскольку все гармоники нижнего звука расположены в целых числах, а согласно (3) первое совпадение происходит на частоте m, получается, что нижний звук внутри прямоугольника даст m звучащих частот.
Нужно учесть, что совпадающую частоту m мы опять посчитали два раза: когда считали частоты верхнего звука и когда считали частоты нижнего звука. Но фактически частота одна, и для правильного ответа одну «лишнюю» частоту нам нужно будет вычесть.
Итого всех звучащих частот внутри прямоугольника получится:
Подставив (2) и (4) в формулу (1), получим простое выражение для расчета консонанса:
Чтобы подчеркнуть, консонанс каких именно звуков мы рассчитали, можно указать эти звуки в скобках у cons:
С помощью такой простой формулы можно посчитать консонанс любого интервала.
А теперь рассмотрим некоторые свойства частотного консонанса и примеры его расчета.
Свойства и примеры
Для начала рассчитаем консонансы для самых простых интервалов и убедимся, что формула (6) «работает».
Какой интервал является самым простым?
Безусловно, прима. Две ноты звучат в унисон. На графике это будет выглядеть так:
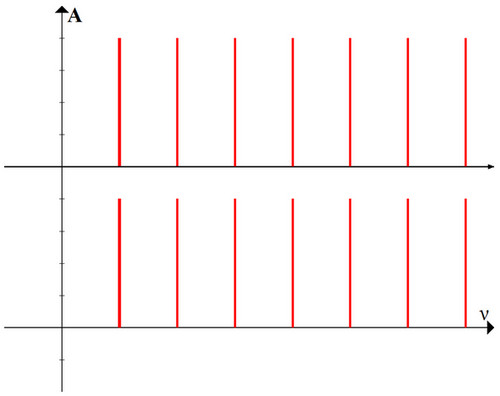
Мы видим, что совпадают абсолютно все звучащие частоты. Следовательно, консонанс должен быть равен:
Теперь подставим соотношение для унисона  в формулу (6), получим:
в формулу (6), получим:
Расчет совпадает с «интуитивным» ответом, что и следовало ожидать.
Возьмем другой пример, в котором интуитивный ответ так же очевиден, — октаву.
В октаве верхний звук в 2 раза выше нижнего (по частоте основного тона), соответственно, на графике это будет выглядеть так:
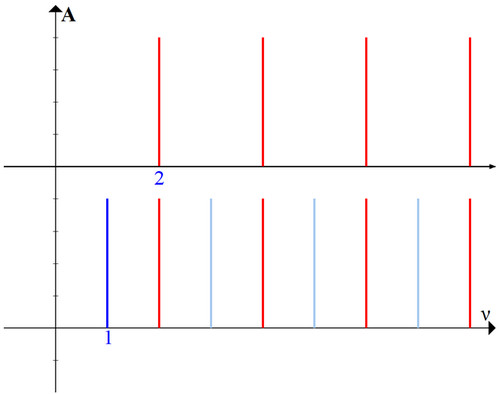
Из графика видно, что совпадает каждая вторая гармоника, и интуитивный ответ: консонанс равен 50%.
Посчитаем его по формуле (6):
И вновь расчетная величина равна «интуитивной».
Если возьмем в качестве нижнего звука ноту до и отложим на графике величину консонанса для всех интервалов внутри октавы (простых интервалов), то получим такую картину:

Самые высокие показатели меры консонанса у октавы, квинты и кварты. Они исторически относились к «совершенным» консонансам. Показатели малой и большой терций, и малой и большой секст чуть ниже, эти интервалы считаются «несовершенными» консонансами. Остальные интервалы имеют более низкую меру консонанса, традиционно они относятся к группе диссонансов.
Теперь перечислим некоторые свойства меры частотного консонанса, которые исходят из формулы для её расчета:
- Чем сложнее соотношение
 (чем больше числа m и n), тем менее консонантен интервал.
(чем больше числа m и n), тем менее консонантен интервал.
И m и n в формуле (6) находятся в знаменателе, следовательно, при увеличении этих чисел мера консонанса уменьшается.
- Консонанс интервала вверх равен консонансу интервала вниз.
Чтобы получить вместо интервала вверх интервал вниз, нам нужно в соотношении  поменять местами m и n. Но в формуле (6) от такой замены ровным счетом ничего не поменяется.
поменять местами m и n. Но в формуле (6) от такой замены ровным счетом ничего не поменяется.
- Мера частотного консонанса интервала не зависит от того, от какой ноты мы его строим.
Если сместить обе ноты на одинаковый интервал вверх или вниз (например, построить квинту не от ноты до, а от ноты ре), то соотношение  между нотами не изменится, а следовательно, и мера частотного консонанса останется прежней.
между нотами не изменится, а следовательно, и мера частотного консонанса останется прежней.
Можно было бы привести и другие свойства консонанса, но пока ограничимся этими.
Физика и лирика
Рисунок 7 даёт нам представление о том, как устроен консонанс. Но так ли мы на самом деле воспринимаем консонанс интервалов? Существуют ли люди, которым не нравятся совершенные консонансы, а самые диссонантные созвучия кажутся приятными?
Да, такие люди, безусловно, есть. И для того, чтобы это объяснить, следует разграничить два понятия: физический консонанс и консонанс воспринимаемый.
Всё, что мы рассматривали в данной статье, имеет отношение к физическому консонансу. Для его расчета необходимо знать, как устроен звук, и как складываются разные колебания. Физический консонанс даёт предпосылки для консонанса воспринимаемого, но не обуславливает его на 100%.
Консонанс воспринимаемый определяется очень просто. Человека спрашивают, нравится ли ему данное созвучие. Если да – значит, для него это консонанс, если нет – диссонанс. Если ему дают на сравнение два интервала, то можно сказать, что один из них покажется человеку в данный момент более консонансным, другой менее.
Можно ли посчитать воспринимаемый консонанс? Даже если предположить, что можно, то расчет этот будет катастрофически сложным, в него будет входить ещё одна бесконечность – бесконечность человека: его опыт, особенности слуха и способности мозга. С этой бесконечностью так просто не справиться.
Однако исследования в этой области ведутся. В частности, композитор Иван Сошинский, любезно предоставляющий аудиоматериалы для данных заметок, разработал программу, с помощью которой можно для каждого человека построить его индивидуальную карту восприятия консонансов. Сейчас ведется разработка сайта mu-theory.info, на котором любой желающий сможет пройти тестирование и узнать особенности своего слуха.
И всё же, если есть воспринимаемый консонанс, и он отличается от физического, какой же смысл в расчете последнего? Можно переформулировать этот вопрос в более конструктивном ключе: как соотносятся эти два понятия?
Исследования показывают, что корреляция между усредненным воспринимаемым консонансом и физическим консонансом порядка 80%. Это означает, что у каждого человека могут быть свои индивидуальные особенности, но подавляющий вклад в определение консонанса вносит физика звука.
Разумеется, научные изыскания в этой области находятся ещё в самом начале. И в качестве структуры звука мы взяли сравнительно простую модель кратных гармоник, и расчет консонанса применяли самый простой – частотный, и не учитывали особенности деятельности мозга по обработке звукового сигнала. Но то, что даже в рамках таких упрощений получена очень высокая степень корреляции теории и эксперимента, весьма обнадеживает и дает стимул к дальнейшим исследованиям.
Применение научного метода в области музыкальной гармонии не ограничивается расчетом консонанса, оно дает и более интересные плоды.
Например, с помощью научного метода можно музыкальную гармонию изобразить графически, визуализировать. О том, как это сделать, мы поговорим в следующий раз.
Автор – Роман Олейников





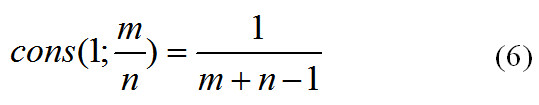
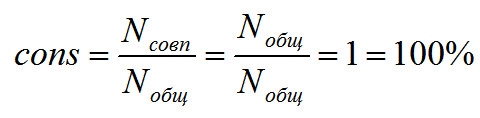
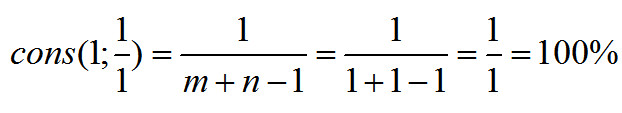
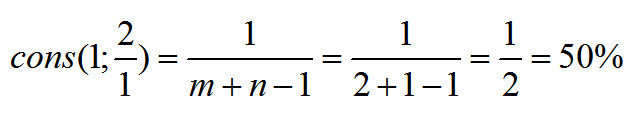
Идея иетересая. Все же, физические теории (а это чем-то похоже на физ. теорию) принято проверять на реальных примерах.Так вот, мне интересно, как пометить консонантность интервалов равномерное темперированного строя. Они же иррациональные. Ну, максимум, цепными дробями представить можно, но тогда они все имеют грубо говоря нулевую консонантность.
Евгений, спасибо за вопрос. В строгом смысле в этом приближении мера консонанса для темперированных интервалов равна 0, т.к. ни один обертон совпадать не будет. Но гармоники звука не строго монохромны, и к тому же наше ухо — не идеальный измерительный прибор, поэтому теорию сравнительно легко расширить на иррациональные отношения. Если интересна эта тема, могу порекомендовать лекцию про консонанс на нашем канале (https://www.youtube.com/watch?v=3u7uBmDxtyQ&t=2271s), в ней разобран этот случай, и довольно много про экспериментальные подтверждения теории.