Самый сильный диссонанс

Что такое диссонанс? Простыми словами – это неблагозвучное, неприятное сочетание различных звуков. Почему же такие сочетания присутствуют среди интервалов и аккордов? Откуда они взялись и зачем они нужны?

Путешествие Одиссея

Как мы выяснили в предыдущей заметке, во времена Античности господствовал пифагорейский строй. В нем все звуки строя получаются простым делением струны на 2 или на 3 равные части. Деление на две части просто смещает звук на октаву. А вот деление на три рождает новые ноты.

Возникает законный вопрос: а когда нам прекратить это деление? Из каждой новой ноты, поделив струну на 3, мы можем получить ещё одну. Таким образом мы можем получить в музыкальной системе 1000 или 100000 звуков. Где же нам стоит остановиться?

Когда Одиссей, герой древнегреческой поэмы, возвращался на свою Итаку, его на пути ждало множество препятствий. И каждое из них задерживало его в путешествии до тех пор, пока он не находил, как с ним справиться.

На пути развития музыкальных систем тоже возникали свои препятствия. Они на какое-то время затормаживали процесс появления новых нот, затем их преодолевали и плыли дальше, где встречали следующую преграду. Этими преградами были диссонансы.

Попробуем понять, что такое диссонанс.

Точное определение этого явления мы сможем получить, когда поймем физическое устройство звука. Но сейчас точность нам не требуется, нам достаточно объяснить это простыми словами.

Итак, у нас есть струна. Мы можем поделить ее на 2 или на 3 части. Получим таким образом октаву и дуодециму. Октава звучит более консонантно, и это понятно – деление на 2 проще, чем деление на 3. В свою очередь дуодецима будет звучать консонантней, чем струна поделенная на 5 частей (такое деление даст терцию через две октавы), потому что деление на 3 проще, чем деление на 5.

Теперь вспомним, как строилась, например, квинта. Мы делили струну на 3 части, а затем увеличивали получившуюся длину в 2 раза (рис.1).

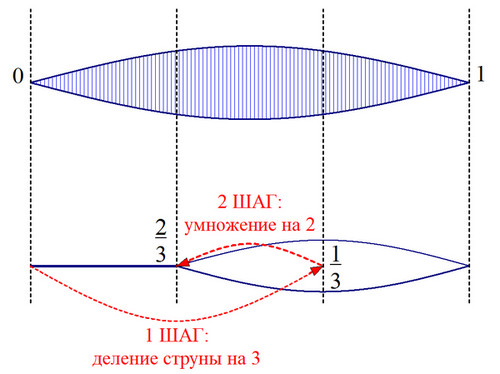
Как видим, чтобы построить квинту, нам нужно сделать не один, а два шага, а, следовательно, квинта будет звучать менее консонантно, чем октава или дуодецима. С каждым шагом мы как бы всё дальше и дальше уходим от исходной ноты.

Можно сформулировать простое правило для определения консонантности:

чем меньше шагов мы делаем, и чем проще сами эти шаги, тем консонантней будет интервал.

Вернемся к построениям.

Итак, люди выбрали первый звук (будем для удобства считать, что это до, хотя сами древние греки так его не называли) и начали строить другие ноты, деля или умножая длину струны на 3.

Сначала получили два звука, которые к до оказались самыми близкими – это фа и соль (рис.2). Соль получается, если длину струны уменьшить в 3 раза, а фа – наоборот, если в 3 раза увеличить.

Индекс π по-прежнему будет означать, что речь идет о нотах пифагорейского строя.

Если перенести эти ноты в ту же октаву, где расположена нота до, то интервалы до них будут называться кварта (до-фа) и квинта (до-соль). Это два весьма примечательных интервала. При переходе от пифагорейского строя к натуральному, когда изменились почти все интервалы, построение кварты и квинты осталось неизменным. Формирование тональности шло с самым непосредственным участием этих нот, именно на них строились доминанта и субдоминанта. Эти интервалы оказались настолько консонантными, что господствовали в музыке вплоть до эпохи романтизма, да и после им отводилась весьма значительная роль.

Но мы отвлеклись от диссонансов. На этих трех нотах построения не остановились. Сруну продолжили делить на 3 части и дуодецима за дуодецимой получать новые и новые звуки.

Первое препятствие возникло на пятом шаге, когда к до (исходная нота), ре, фа, соль, ля добавилась нота ми (рис.3).

Между нотами ми и фа образовался интервал, который показался людям того времени жутко диссонантным. Этим интервалом была малая секунда.

Малая секунда ми-фа — гармоническая

* * * * *

Встретив этот интервал, решили, что включать ми в систему уже не стоит, надо остановиться на 5 нотах. Так первая система оказалась 5-нотной, ее назвали пентатоника. Все интервалы в ней весьма консонантны. Пентатонику до сих пор можно встретить в народной музыке. Иногда как особая краска она присутствует и в классике.

Со временем к звучанию малой секунды привыкли и поняли, что если использовать ее умеренно и к месту, то с ней вполне можно жить. И следующим препятствием стал шаг номер 7 (рис.4).

Новая нота оказалась настолько диссонантной, что ей даже решили не давать собственного названия, а назвали фа-диез (обозначается f#). Собственно диез и означает тот интервал, который образовался между этими двумя нотами: фа и фа-диез. Звучит он так:

Интервал фа и фа-диез — гармонический

* * * * *

Если не выходить «за пределы диеза», то у нас получается 7-нотный строй – диатоника. Большинство классических и современных музыкальных систем являются 7-ступенными, то есть наследуют в этом отношении пифагорейской диатонике.

Несмотря на такое огромное значение диатоники, Одиссей поплыл дальше. Преодолев преграду в виде диеза, он увидел открытый простор, в котором можно набрать в систему целых 12 нот. Но вот 13-ая образовывала страшный диссонанс – пифагорову комму.

Пифагорова комма

* * * * *

Пожалуй, можно сказать, что комма явила собой Сциллу и Харибду в одном лице. На преодоление этого препятствия ушли не годы и даже не столетия. Только спустя пару тысяч лет, в XX веке нашей эры, музыканты всерьез обратились к микрохроматическим системам, которые содержат больше 12 нот. Разумеется, на протяжении этих веков предпринимались отдельные попытки добавить в октаву ещё несколько звуков, но попытки эти были настолько робкими, что говорить о их значительном вкладе в музыкальную культуру, к сожалению, не приходится.

Можно ли считать попытки XX века в полной мере удачными? Вошли ли микрохроматические системы в музыкальный обиход? Вернемся к этому вопросу, но перед этим рассмотрим ещё несколько диссонансов уже не из пифагорейского строя.

Волк и дьявол

Когда мы приводили диссонантные интервалы из пифагорейского строя, мы немного лукавили. То есть и малая секунда и диез были, но слышали их тогда немного иначе.

Дело в том, что музыка античности по преимуществу была монодического склада. Проще говоря, одновременно звучала только одна нота, а вертикаль – одновременное сочетание нескольких звуков – почти не использовалась. Поэтому и малую секунду и диез античные любители музыки, как правило, слышали так:

Малая секунда ми-фа — мелодическая

* * * * *

Полутон фа и фа-диез — мелодический

* * * * *

А вот с развитием вертикали в полной мере зазвучали гармонические (вертикальные) интервалы, в том числе и диссонантные.

Первым в этом ряду стоит назвать тритон.

Так звучит тритон

* * * * *

Тритоном он называется, не потому что он похож на земноводное, а потому что в нем от нижнего звука до верхнего ровно три целых тона (то есть шесть полутонов, шесть клавиш фортепиано). Интересно, что и на латыни он называется tritonus.

Этот интервал можно построить и в пифагорейском строе и в натуральном. И там и там он будет звучать диссонантно.

Чтобы построить его в пифагорейском строе придется поделить струну на 3 части 6 раз, а затем получившуюся длину 10 раз увеличить вдвое. Получится, что длина струны будет выражаться дробью 729/1024. Стоит ли говорить, что при таком количестве шагов о консонансе говорить не приходится.

В натуральном строе ситуация немногим лучше. Натуральный тритон можно получить так: два раза поделить длину струны на 3 (т.е. делим на 9), затем поделить еще на 5 (итого делим на 45 частей), а потом 5 раз увеличить вдвое. В результате длина струны будет 32/45, что хоть и немного проще, но консонанса не сулит.

По слухам в средневековье этот интервал назывался «дьяволом в музыке».

Но важнее для развития музыки оказалось другое созвучие – волчья квинта.

Волчья квинта

* * * * *

Откуда же такой интервал берется? Зачем он нужен?

Предположим мы набираем звуки в натуральный строй от ноты до. В нем нота ре получается, если мы два раза поделим сруну на 3 части (сделаем два дуодецимальных шага вперед). А нота ля образуется несколько иначе: для ее получения нам нужно увеличить струну в 3 раза (сделать по дуодецимам один шаг назад), а затем поделить получившуюся длину струны на 5 частей (то есть взять натуральную терцию, которой как раз и не было в пифагорейском строе). В результате между длинами струн нот ре и ля мы получим не простое соотношение 2/3 (чистую квинту), а соотношение 40/27 (волчью квинту). Как видим из соотношения, это созвучие и не может быть консонантным.

А почему бы нам не взять ноту ля, которая бы составляла чистую квинту от ре? Дело в том, что тогда у нас появятся две ноты ля – «квинтовая от ре» и «натуральная». Но с «квинтовой» ля возникнут те же проблемы, что были с ре – ей понадобится своя квинта, и у нас появятся уже две ноты ми.

И этот процесс неостановим. На месте одной головы гидры появляется две. Решив одну проблему, мы порождаем новую.

Решение проблемы волчьих квинт оказалось радикальным. Создали равномерно темперированный строй, где и «квинтовая» ля и «натуральная» заменились одной нотой – темперированной ля, которая давала чуть-чуть фальшивые интервалы со всеми другими нотами, но при этом фальшь была едва заметной, а не столь очевидной, как в волчьей квинте.

Так волчья квинта, как опытный морской волк, привела музыкальный корабль к весьма неожиданным берегам – равномерно темперированному строю.

Краткая история диссонансов

Чему же нас учит краткая история диссонансов? Какой опыт можно извлечь из путешествия длиною в несколько веков?

• Во-первых, как оказалось, диссонансы в истории музыки играли ничуть не меньшую роль, чем консонансы. При том, что они не нравились и с ними боролись, именно они зачастую давали толчок к появлению новых музыкальных направлений, служили катализатором неожиданных открытий.
• Во-вторых, можно обнаружить интересную тенденцию. С развитием музыки люди учатся слышать консонанс во всё более и более сложных сочетаниях звуков.

Мало кто сейчас будет считать малую секунду таким уж диссонантным интервалом, особенно в мелодическом расположении. А ведь всего каких-нибудь две с половиной тысячи лет назад это было так. И тритон вошел в музыкальную практику, многие музыкальные произведения, даже в популярной музыке, строятся с самым серьезным участием тритона.

Например, с тритонов начинается композиция Джими Хендрикса Purple Haze:

Постепенно всё больше и больше диссонансов переходят в разряд «не таких уж и диссонансов» или «почти консонансов». Дело не в том, что наш слух испортился, и мы не слышим, что звучание таких интервалов и аккордов резкое или отталкивающее. Дело в том, что наш музыкальный опыт растет, и сложные многошаговые построения мы уже можем воспринимать как необычные, неординарные и по-своему интересные.

Есть музыканты, которым и волчьи квинты или коммы, представленные в данной статье, не покажутся ужасающими, они отнесутся к ним как к своеобразному, сложному материалу, с которым можно поработать в создании столь же сложной и своеобразной музыки.

Автор – Роман Олейников
Аудиозаписи — Иван Сошинский